ree FTP and Download Manager 6.1.0.1

View screenshots

Developer Softwareclub.ws [view all products from developer] Date Added February 7, 2007, 11:34 GMT License Free (Freeware) Week / All Time Downloads 27 / 6,177 Filename / Size scftp6101.exe / 144K OS Support Windows All

Johannes Kepler: The
Laws of Planetary Motion 

---

In the interplay between quantitative observation and theoretical construction that characterizes the development of modern science, we have seen that Brahe was the master of the first but was deficient in the second. The next great development in the history of astronomy was the theoretical intuition of Johannes Kepler (1571-1630), a German who went to Prague to become Brahe's assistant.

Brahe's Data and Kepler

Kepler and Brahe did not get along well. Brahe apparently mistrusted Kepler, fearing that his bright young assistant might eclipse him as the premiere astonomer of his day. He therefore let Kepler see only part of his voluminous data.He set Kepler the task of understanding the orbit of the planet Mars, which was particularly troublesome. It is believed that part of the motivation for giving the Mars problem to Kepler was that it was difficult, and Brahe hoped it would occupy Kepler while Brahe worked on his theory of the Solar System. In a supreme irony, it was precisely the Martian data that allowed Kepler to formulate the correct laws of planetary motion, thus eventually achieving a place in the development of astronomy far surpassing that of Brahe.

Kepler and the Elliptical Orbits

Unlike Brahe, Kepler believed firmly in the Copernican system. In retrospect, the reason that the orbit of Mars was particularly difficult was that Copernicus had correctly placed the Sun at the center of the Solar System, but had erred in assuming the orbits of the planets to be circles. Thus, in the Copernican theory epicycles were still required to explain the details of planetary motion.It fell to Kepler to provide the final piece of the puzzle: after a long struggle, in which he tried mightily to avoid his eventual conclusion, Kepler was forced finally to the realization that the orbits of the planets were not the circles demanded by Aristotle and assumed implicitly by Copernicus, but were instead the "flattened circles" that geometers call ellipses (See adjacent figure; the planetary orbits are only slightly elliptical and are not as flattened as in this example.)
The irony noted above lies in the realization that the difficulties with the Martian orbit derive precisely from the fact that the orbit of Mars was the most elliptical of the planets for which Brahe had extensive data. Thus Brahe had unwittingly given Kepler the very part of his data that would allow Kepler to eventually formulate the correct theory of the Solar System and thereby to banish Brahe's own theory!

Some Properties of Ellipses

Since the orbits of the planets are ellipses, let us review a few basic properties of ellipses.1. For an ellipse there are two points called foci (singular: focus) such that the sum of the distances to the foci from any point on the ellipse is a constant. In terms of the diagram shown to the left, with "x" marking the location of the foci, we have the equation

a + b = constant

that defines the ellipse in terms of the distances a and b.2. The amount of "flattening" of the ellipse is termed the eccentricity. Thus, in the following figure the ellipses become more eccentric from left to right. A circle may be viewed as a special case of an ellipse with zero eccentricity, while as the ellipse becomes more flattened the eccentricity approaches one. Thus, all ellipses have eccentricities lying between zero and one.
The orbits of the planets are ellipses but the eccentricities are so small for most of the planets that they look circular at first glance. For most of the planets one must measure the geometry carefully to determine that they are not circles, but ellipses of small eccentricity. Pluto and Mercury are exceptions: their orbits are sufficiently eccentric that they can be seen by inspection to not be circles.3. The long axis of the ellipse is called the major axis, while the short axis is called the minor axis (adjacent figure). Half of the major axis is termed asemimajor axis. The length of a semimajor axis is often termed the size of the ellipse. It can be shown that the average separation of a planet from the Sun as it goes around its elliptical orbit is equal to the length of the semimajor axis. Thus, by the "radius" of a planet's orbit one usually means the length of the semimajor axis.

The Laws of Planetary Motion

Kepler obtained Brahe's data after his death despite the attempts by Brahe's family to keep the data from him in the hope of monetary gain. There is some evidence that Kepler obtained the data by less than legal means; it is fortunate for the development of modern astronomy that he was successful. Utilizing the voluminous and precise data of Brahe, Kepler was eventually able to build on the realization that the orbits of the planets were ellipses to formulate his Three Laws of Planetary Motion.

Kepler's First Law:

I. The orbits of the planets are ellipses, with the Sun at one focus of the ellipse.

Kepler's First Law is illustrated in the image shown above. The Sun is not at the center of the ellipse, but is instead at one focus (generally there is nothing at the other focus of the ellipse). The planet then follows the ellipse in its orbit, which means that the Earth-Sun distance is constantly changing as the planet goes around its orbit. For purpose of illustration we have shown the orbit as rather eccentric; remember that the actual orbits are much less eccentric than this.

Kepler's Second Law:

II. The line joining the planet to the Sun sweeps out equal areas in equal times as the planet travels around the ellipse.

Kepler's second law is illustrated in the preceding figure. The line joining the Sun and planet sweeps out equal areas in equal times, so the planet moves faster when it is nearer the Sun. Thus, a planet executes elliptical motion with constantly changing angular speed as it moves about its orbit. The point of nearest approach of the planet to the Sun is termed perihelion; the point of greatest separation is termed aphelion. Hence, by Kepler's second law, the planet moves fastest when it is near perihelion and slowest when it is near aphelion. 

Kepler's Third Law:

III. The ratio of the squares of the revolutionary periods for two planets is equal to the ratio of the cubes of their semimajor axes:

In this equation P represents the period of revolution for a planet and R represents the length of its semimajor axis. The subscripts "1" and "2" distinguish quantities for planet 1 and 2 respectively. The periods for the two planets are assumed to be in the same time units and the lengths of the semimajor axes for the two planets are assumed to be in the same distance units.
Kepler's Third Law implies that the period for a planet to orbit the Sun increases rapidly with the radius of its orbit. Thus, we find that Mercury, the innermost planet, takes only 88 days to orbit the Sun but the outermost planet (Pluto) requires 248 years to do the same.

Calculations Using Kepler's Third Law

A convenient unit of measurement for periods is in Earth years, and a convenient unit of measurement for distances is the average separation of the Earth from the Sun, which is termed an astronomical unit and is abbreviated as AU. If these units are used in Kepler's 3rd Law, the denominators in the preceding equation are numerically equal to unity and it may be written in the simple form

This equation may then be solved for the period P of the planet, given the length of the semimajor axis,

or for the length of the semimajor axis, given the period of the planet,

As an example of using Kepler's 3rd Law, let's calculate the "radius" of the orbit of Mars (that is, the length of the semimajor axis of the orbit) from the orbital period. The time for Mars to orbit the Sun is observed to be 1.88 Earth years. Thus, by Kepler's 3rd Law the length of the semimajor axis for the Martian orbit is

which is exactly the measured average distance of Mars from the Sun. As a second example, let us calculate the orbital period for Pluto, given that its observed average separation from the Sun is 39.44 astronomical units. From Kepler's 3rd Law

which is indeed the observed orbital period for the planet Pluto.

Universal Law of Gravitation

---

Sir Isaac Newton: The
Universal Law of Gravitation 

---

There is a popular story that Newton was sitting under an apple tree, an apple fell on his head, and he suddenly thought of the Universal Law of Gravitation. As in all such legends, this is almost certainly not true in its details, but the story contains elements of what actually happened.

What Really Happened with the Apple?

Probably the more correct version of the story is that Newton, upon observing an apple fall from a tree, began to think along the following lines: The apple is accelerated, since its velocity changes from zero as it is hanging on the tree and moves toward the ground. Thus, by Newton's 2nd Law there must be a force that acts on the apple to cause this acceleration. Let's call this force "gravity", and the associated acceleration the "accleration due to gravity". Then imagine the apple tree is twice as high. Again, we expect the apple to be accelerated toward the ground, so this suggests that this force that we call gravity reaches to the top of the tallest apple tree.

Sir Isaac's Most Excellent Idea

Now came Newton's truly brilliant insight: if the force of gravity reaches to the top of the highest tree, might it not reach even further; in particular, might it not reach all the way to the orbit of the Moon! Then, the orbit of the Moon about the Earth could be a consequence of the gravitational force, because the acceleration due to gravity could change the velocity of the Moon in just such a way that it followed an orbit around the earth.This can be illustrated with the thought experiment shown in the following figure. Suppose we fire a cannon horizontally from a high mountain; the projectile will eventually fall to earth, as indicated by the shortest trajectory in the figure, because of the gravitational force directed toward the center of the Earth and the associated acceleration. (Remember that an acceleration is a change in velocity and that velocity is a vector, so it has both a magnitude and a direction. Thus, an acceleration occurs if either or both the magnitude and the direction of the velocity change.)

But as we increase the muzzle velocity for our imaginary cannon, the projectile will travel further and further before returning to earth. Finally, Newton reasoned that if the cannon projected the cannon ball with exactly the right velocity, the projectile would travel completely around the Earth, always falling in the gravitational field but never reaching the Earth, which is curving away at the same rate that the projectile falls. That is, the cannon ball would have been put into orbit around the Earth. Newton concluded that the orbit of the Moon was of exactly the same nature: the Moon continuously "fell" in its path around the Earth because of the acceleration due to gravity, thus producing its orbit.By such reasoning, Newton came to the conclusion that any two objects in the Universe exert gravitational attraction on each other, with the force having a universal form:

The constant of proportionality G is known as the universal gravitational constant. It is termed a "universal constant" because it is thought to be the same at all places and all times, and thus universally characterizes the intrinsic strength of the gravitational force.

The Center of Mass for a Binary System

If you think about it a moment, it may seem a little strange that in Kepler's Laws the Sun is fixed at a point in space and the planet revolves around it. Why is the Sun privileged? Kepler had rather mystical ideas about the Sun, endowing it with almost god-like qualities that justified its special place. However Newton, largely as a corollary of his 3rd Law, demonstrated that the situation actually was more symmetrical than Kepler imagined and that the Sun does not occupy a privileged postion; in the process he modified Kepler's 3rd Law.Consider the diagram shown to the right. We may define a point called the center of mass between two objects through the equations

where R is the total separation between the centers of the two objects. The center of mass is familiar to anyone who has ever played on a see-saw. The fulcrum point at which the see-saw will exactly balance two people sitting on either end is the center of mass for the two persons sitting on the see-saw.Here is a Center of Mass Calculator that will help you make and visualize calculations concerning the center of mass. (Caution: this applet is written under Java 1.1, which is only supported by the most recent browsers. It should work on Windows systems under Netscape 4.06 or the most recent version of Internet Explorer 4.0, but may not yet work on Mac or Unix systems or earlier Windows browsers.)

Newton's Modification of Kepler's Third Law

Because for every action there is an equal and opposite reaction, Newton realized that in the planet-Sun system the planet does not orbit around a stationary Sun. Instead, Newton proposed that both the planet and the Sun orbited around the common center of mass for the planet-Sun system. He then modified Kepler's 3rd Law to read,

where P is the planetary orbital period and the other quantities have the meanings described above, with the Sun as one mass and the planet as the other mass. (As in the earlier discussion of Kepler's 3rd Law, this form of the equation assumes that masses are measured in solar masses, times in Earth years, and distances in astronomical units.) Notice the symmetry of this equation: since the masses are added on the left side and the distances are added on the right side, it doesn't matter whether the Sun is labeled with 1 and the planet with 2, or vice-versa. One obtains the same result in either case.Now notice what happens in Newton's new equation if one of the masses (either 1 or 2; remember the symmetry) is very large compared with the other. In particular, suppose the Sun is labeled as mass 1, and its mass is much larger than the mass for any of the planets. Then the sum of the two masses is always approximately equal to the mass of the Sun, and if we take ratios of Kepler's 3rd Law for two different planets the masses cancel from the ratio and we are left with the original form of Kepler's 3rd Law:

Thus Kepler's 3rd Law is approximately valid because the Sun is much more massive than any of the planets and therefore Newton's correction is small. The data Kepler had access to were not good enough to show this small effect. However, detailed observations made after Kepler show that Newton's modified form of Kepler's 3rd Law is in better accord with the data than Kepler's original form.

Two Limiting Cases

We can gain further insight by considering the position of the center of mass in two limits. First consider the example just addressed, where one mass is much larger than the other. Then, we see that the center of mass for the system essentially concides with the center of the massive object:

This is the situation in the Solar System: the Sun is so massive compared with any of the planets that the center of mass for a Sun-planet pair is always very near the center of the Sun. Thus, for all practical purposes the Sun IS almost (but not quite) motionless at the center of mass for the system, as Kepler originally thought.However, now consider the other limiting case where the two masses are equal to each other. Then it is easy to see that the center of mass lies equidistant from the two masses and if they are gravitationally bound to each other, each mass orbits the common center of mass for the system lying midway between them:

This situation occurs commonly with binary stars (two stars bound gravitationally to each other so that they revolve around their common center of mass). In many binary star systems the masses of the two stars are similar and Newton's correction to Kepler's 3rd Law is very large.Implements Newton's modified form of Kepler's 3rd law for two objects (planets or stars) revolving around their common center of mass. By making one mass much larger than the other in this interactive animation you can illustrate the ideas discussed above and recover Kepler's original form of his 3rd Law where a less massive object appears to revolve around a massive object fixed at one focus of an ellipse.
These limiting cases for the location of the center of mass are perhaps familiar from our afore-mentioned playground experience. If persons of equal weight are on a see-saw, the fulcrum must be placed in the middle to balance, but if one person weighs much more than the other person, the fulcrum must be placed close to the heavier person to achieve balance.

Weight and the Gravitational Force

We have seen that in the Universal Law of Gravitation the crucial quantity is mass. In popular language mass and weight are often used to mean the same thing; in reality they are related but quite different things. What we commonly call weight is really just the gravitational force exerted on an object of a certain mass. We can illustrate by choosing the Earth as one of the two masses in the previous illustration of the Law of Gravitation:

Thus, the weight of an object of mass m at the surface of the Earth is obtained by multiplying the mass m by the acceleration due to gravity, g, at the surface of the Earth. The acceleration due to gravity is approximately the product of the universal gravitational constant G and the mass of the Earth M, divided by the radius of the Earth, r, squared. (We assume the Earth to be spherical and neglect the radius of the object relative to the radius of the Earth in this discussion.) The measured gravitational acceleration at the Earth's surface is found to be about 980 cm/second/second.

Mass and Weight

Mass is a measure of how much material is in an object, but weight is a measure of the gravitational force exerted on that material in a gravitational field; thus, mass and weight are proportional to each other, with the acceleration due to gravity as the proportionality constant. It follows that mass is constant for an object (actually this is not quite true, but we will save that surprise for our later discussion of the Relativity Theory), but weight depends on the location of the object. For example, if we transported the preceding object of mass m to the surface of the Moon, the gravitational acceleration would change because the radius and mass of the Moon both differ from those of the Earth. Thus, our object has mass m both on the surface of the Earth and on the surface of the Moon, but it willweigh much less on the surface of the Moon because the gravitational acceleration there is a factor of 6 less than at the surface of the Earth.

Animation1

Average vs. Instantaneous Speed

During a typical trip to school, your car will undergo a series of changes in its speed. If you were to inspect the speedometer readings at regular intervals, you would notice that it changes often. The speedometer of a car reveals information about the instantaneous speed of your car. It shows your speed at a particular instant in time.

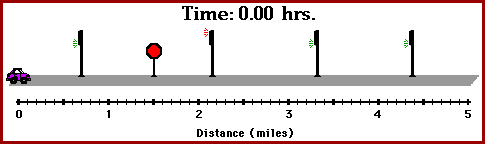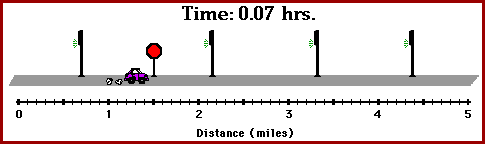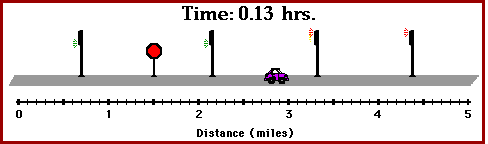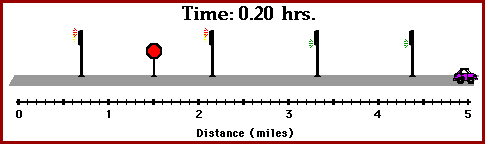
The instantaneous speed of an object is not to be confused with the average speed.Average speed is a measure of the distance traveled in a given period of time; it is sometimes referred to as the distance per time ratio. Suppose that during your trip to school, you traveled a distance of 5 miles and the trip lasted 0.2 hours (12 minutes). The average speed of your car could be determined as

On the average, your car was moving with a speed of 25 miles per hour. During your trip, there may have been times that you were stopped and other times that your speedometer was reading 50 miles per hour. Yet, on average, you were moving with a speed of 25 miles per hour.

Animation

Direction of Acceleration and Velocity

Consider the motion of a Hot Wheels car down an incline, across a level and straight section of track, around a 180-degree curve, and finally along a final straight section of track. Such a motion is depicted in the animation below. The car gains speed while moving down the incline - that is, it accelerates. Along the straight sections of track, the car slows down slightly (due to air resistance forces). Again the car could be described as having an acceleration. Finally, along the 180-degree curve, the car is changing its direction; once more the car is said to have an acceleration due to the change in the direction. Accelerating objects have a changing velocity - either due to a speed change (speeding up or slowing down) or a direction change.

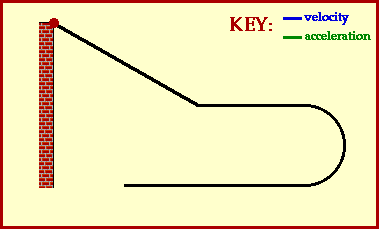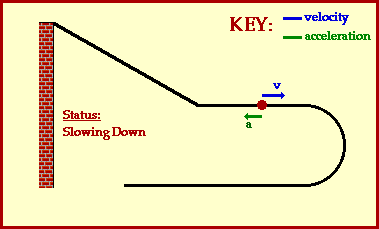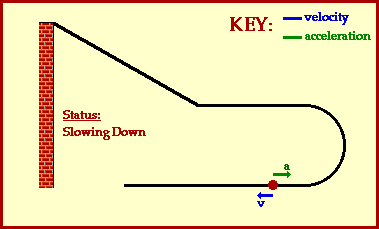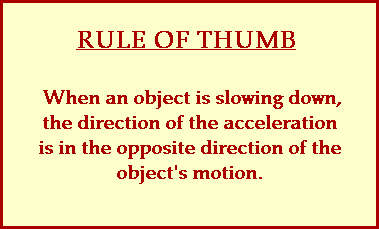
This simple animation above depicts some additional information about the car's motion. The velocity and acceleration of the car are depicted by vector arrows. The direction of these arrows are representative of the direction of the velocity and acceleration vectors. Note that the velocity vector is always directed in the same direction which the car is moving. A car moving eastward would be described as having an eastward velocity. And a car moving westward would be described as having a westward velocity.

The direction of the acceleration vector is not so easily determined. As shown in the animation, an eastward heading car can have a westward directed acceleration vector. And a westward heading car can have an eastward directed acceleration vector. So how can the direction of the acceleration vector be determined? A simple rule of thumb for determining the direction of the acceleration is that an object which is slowing down will have an acceleration directed in the direction opposite of its motion. Applying this rule of thumbwould lead us to conclude that an eastward heading car can have a westward directed acceleration vector if the car is slowing down.

Be careful when discussing the direction of the acceleration of an object; slow down, apply some thought and use the rule of thumb.

Answer2

Seymour has an average speed of

(95 yd) / (10 min) = 9.5 yd/min

and an average velocity of

(55 yd, left) / (10 min) = 5.5 yd/min, left

Answer1

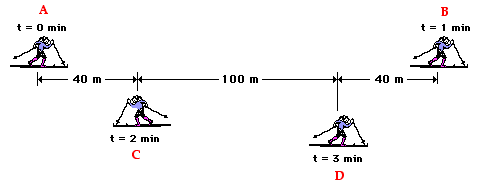
The skier has an average speed of

(420 m) / (3 min) = 140 m/min

and an average velocity of

(140 m, right) / (3 min) = 46.7 m/min, right

Speed and Velocity

Speed and Velocity

Just as distance and displacement have distinctly different meanings (despite their similarities), so do speed and velocity. Speed is a scalar quantity that refers to "how fast an object is moving." Speed can be thought of as the rate at which an object covers distance. A fast-moving object has a high speed and covers a relatively large distance in a short amount of time. A slow-moving object has a low speed and covers a relatively small amount of distance in a short amount of time. An object with no movement at all has a zero speed.

Velocity is a vector quantity that refers to "the rate at which an object changes its position." Imagine a person moving rapidly - one step forward and one step back - always returning to the original starting position. While this might result in a frenzy of activity, it would result in a zero velocity. Because the person always returns to the original position, the motion would never result in a change in position. Since velocity is defined as the rate at which the position changes, this motion results in zero velocity. If a person in motion wishes to maximize their velocity, then that person must make every effort to maximize the amount that they are displaced from their original position. Every step must go into moving that person further from where he or she started. For certain, the person should never change directions and begin to return to the starting position.

Velocity is a vector quantity. As such, velocity is direction aware. When evaluating the velocity of an object, one must keep track of direction. It would not be enough to say that an object has a velocity of 55 mi/hr. One must include direction information in order to fully describe the velocity of the object. For instance, you must describe an object's velocity as being 55 mi/hr, east. This is one of the essential differences between speed and velocity. Speed is a scalar quantity and does not keep track of direction; velocity is a vector quantity and is direction aware.

The task of describing the direction of the velocity vector is easy. The direction of the velocity vector is simply the same as the direction that an object is moving. It would not matter whether the object is speeding up or slowing down. If an object is moving rightwards, then its velocity is described as being rightwards. If an object is moving downwards, then its velocity is described as being downwards. So an airplane moving towards the west with a speed of 300 mi/hr has a velocity of 300 mi/hr, west. Note that speed has no direction (it is a scalar) and the velocity at any instant is simply the speed value with a direction.

As an object moves, it often undergoes changes in speed. For example, during an average trip to school, there are many changes in speed. Rather than the speed-o-meter maintaining a steady reading, the needle constantly moves up and down to reflect the stopping and starting and the accelerating and decelerating. One instant, the car may be moving at 50 mi/hr and another instant, it might be stopped (i.e., 0 mi/hr). Yet during the trip to school the person might average 32 mi/hr. The average speed during an entire motion can be thought of as the average of all speedometer readings. If the speedometer readings could be collected at 1-second intervals (or 0.1-second intervals or ... ) and then averaged together, the average speed could be determined. Now that would be a lot of work. And fortunately, there is a shortcut. Read on.

Calculating Average Speed and Average Velocity

The average speed during the course of a motion is often computed using the following formula:

In contrast, the average velocity is often computed using this formula

Let's begin implementing our understanding of these formulas with the following problem:

Q: While on vacation, Lisa Carr traveled a total distance of 440 miles. Her trip took 8 hours. What was her average speed?

To compute her average speed, we simply divide the distance of travel by the time of travel.

That was easy! Lisa Carr averaged a speed of 55 miles per hour. She may not have been traveling at a constant speed of 55 mi/hr. She undoubtedly, was stopped at some instant in time (perhaps for a bathroom break or for lunch) and she probably was going 65 mi/hr at other instants in time. Yet, she averaged a speed of 55 miles per hour. The above formula represents a shortcut method of determining the average speed of an object.

Average Speed versus Instantaneous Speed

Since a moving object often changes its speed during its motion, it is common to distinguish between the average speed and the instantaneous speed. The distinction is as follows.

• Instantaneous Speed - the speed at any given instant in time.
• Average Speed - the average of all instantaneous speeds; found simply by a distance/time ratio.

You might think of the instantaneous speed as the speed that the speedometer reads at any given instant in time and the average speed as the average of all the speedometer readings during the course of the trip. Since the task of averaging speedometer readings would be quite complicated (and maybe even dangerous), the average speed is more commonly calculated as the distance/time ratio.

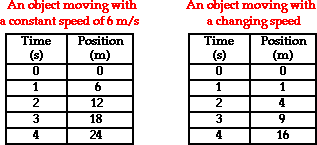
Moving objects don't always travel with erratic and changing speeds. Occasionally, an object will move at a steady rate with a constant speed. That is, the object will cover the same distance every regular interval of time. For instance, a cross-country runner might be running with a constant speed of 6 m/s in a straight line for several minutes. If her speed is constant, then the distance traveled every second is the same. The runner would cover a distance of 6 meters every second. If we could measure her position (distance from an arbitrary starting point) each second, then we would note that the position would be changing by 6 meters each second. This would be in stark contrast to an object that is changing its speed. An object with a changing speed would be moving a different distance each second. The data tables below depict objects with constant and changing speed.

Now let's consider the motion of that physics teacher again. The physics teacher walks 4 meters East, 2 meters South, 4 meters West, and finally 2 meters North. The entire motion lasted for 24 seconds. Determine the average speed and the average velocity.

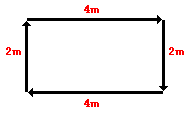
The physics teacher walked a distance of 12 meters in 24 seconds; thus, her average speed was 0.50 m/s. However, since her displacement is 0 meters, her average velocity is 0 m/s. Remember that the displacement refers to the change in position and the velocity is based upon this position change. In this case of the teacher's motion, there is a position change of 0 meters and thus an average velocity of 0 m/s.

Here is another example similar to what was seen before in the discussion of distance and displacement. The diagram below shows the position of a cross-country skier at various times. At each of the indicated times, the skier turns around and reverses the direction of travel. In other words, the skier moves from A to B to C to D.

Use the diagram to determine the average speed and the average velocity of the skier during these three minutes. When finished, click the button to view the answer.

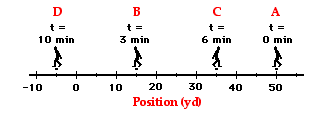
As a last example, consider a football coach pacing back and forth along the sidelines. The diagram below shows several of coach's positions at various times. At each marked position, the coach makes a "U-turn" and moves in the opposite direction. In other words, the coach moves from position A to B to C to D.

What is the coach's average speed and average velocity? When finished, click the button to view the answer.

In conclusion, speed and velocity are kinematic quantities that have distinctly different definitions. Speed, being a scalar quantity, is the rate at which an object covers distance. The average speed is the distance (a scalar quantity) per time ratio. Speed is ignorant of direction. On the other hand, velocity is a vector quantity; it is direction-aware. Velocity is the rate at which the position changes. The average velocity is the displacement or position change (a vector quantity) per time ratio.

Answer3

The displacement of the cars is somewhere near 0 miles since they virtually finish where they started. Yet the successful cars have covered a distance of 500 miles.

Answer2

The displacement of the runners is 0 miles. While they have covered a distance of 10 miles, they are not "out of place" or displaced. They finish where they started. Round-trip motions always have a displacement of 0.

Answer1

The coach covers a distance of

(35 yds + 20 yds + 40 yds) = 95 yards

and has a displacement of 55 yards, left.

Distance and Displacement

Distance and Displacement

Distance and displacement are two quantities that may seem to mean the same thing yet have distinctly different definitions and meanings.

• Distance is a scalar quantity that refers to "how much ground an object has covered" during its motion.
• Displacement is a vector quantity that refers to "how far out of place an object is"; it is the object's overall change in position.

To test your understanding of this distinction, consider the motion depicted in the diagram below. A physics teacher walks 4 meters East, 2 meters South, 4 meters West, and finally 2 meters North.

Even though the physics teacher has walked a total distance of 12 meters, her displacement is 0 meters. During the course of her motion, she has "covered 12 meters of ground" (distance = 12 m). Yet when she is finished walking, she is not "out of place" - i.e., there is no displacement for her motion (displacement = 0 m). Displacement, being a vector quantity, must give attention to direction. The 4 meters east cancels the 4 meters west; and the 2 meters south cancels the 2 meters north. Vector quantities such as displacement are direction aware. Scalar quantities such as distance are ignorant of direction. In determining the overall distance traveled by the physics teachers, the various directions of motion can be ignored.

Now consider another example. The diagram below shows the position of a cross-country skier at various times. At each of the indicated times, the skier turns around and reverses the direction of travel. In other words, the skier moves from A to B to C to D.

Use the diagram to determine the resulting displacement and the distance traveled by the skier during these three minutes. Then click the button to see the answer.

As a final example, consider a football coach pacing back and forth along the sidelines. The diagram below shows several of coach's positions at various times. At each marked position, the coach makes a "U-turn" and moves in the opposite direction. In other words, the coach moves from position A to B to C to D.

What is the coach's resulting displacement and distance of travel? Click the button to see the answer.

To understand the distinction between distance and displacement, you must know the definitions. You must also know that a vector quantity such as displacement is direction-aware and a scalar quantity such as distance is ignorant of direction. When an object changes its direction of motion, displacement takes this direction change into account; heading the opposite direction effectively begins to cancel whatever displacement there once was.

Check Your Understanding

1. What is the displacement of the cross-country team if they begin at the school, run 10 miles and finish back at the school?

2. What is the distance and the displacement of the race car drivers in the Indy 500?